I think 3D geometry has a lot of quirks and has so many results that un_intuitively don’t hold up. In the link I share a discussion with ChatGPT where I asked the following:
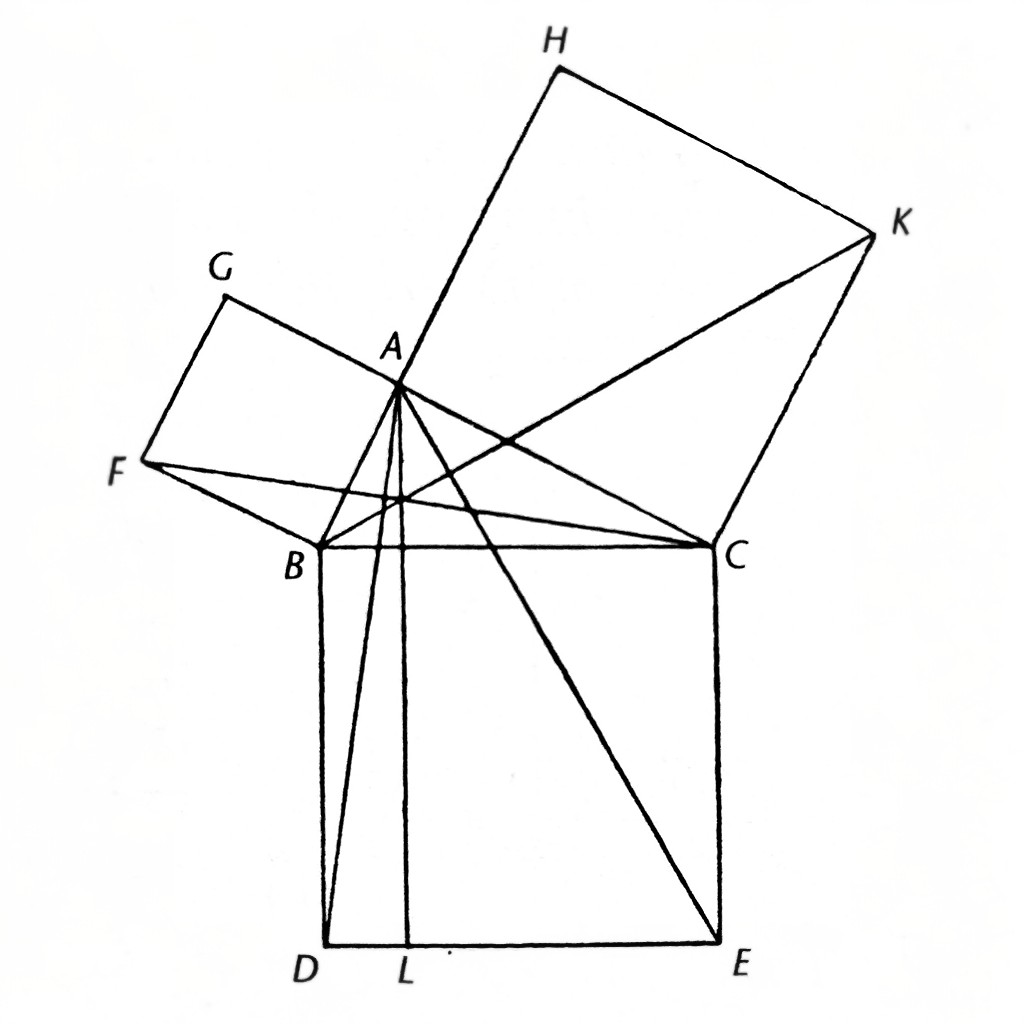
assume a plane defined by a point A=(x_0,y_0,z_0), and normal vector n=(a,b,c) which doesn’t matter here, suppose a point P=(x,y,z) also sitting on the space R^3. Question is:
If H is a point on the plane such that (AH) is perpendicular to (PH), does it follow immediately that H is the projection of P on the plane ?
I suspected the answer is no before asking, but GPT gives the wrong answer “yes”, then corrects it afterwards.
So Don’t we need more education about the 3D space in highschools really? It shouldn’t be that hard to recall such simple properties on the fly, even for the best knowledge retrieving tool at the moment.
While 3D geometry is more difficult for me than 2D, I could almost immediately tell that the answer is no, there are infinitely many points H that satisfy this. The reason it’s unintuitive is that our intuition about what “perpendicular” means comes from 2D and poorly translates to 3D.
The most intuitive explanation I can muster is this: imagine all possible planes that pass through both A and P. It should be obvious that there are infinitely many of them (I visualize it as a plane “rotating” around the AP axis). Each of these planes intersects the given plane since it passes through A. Think of the intersection line. It never passes through P (unless P is on the plane), so it is always possible to draw a perpendicular line from P to that intersection line. With one exception (when the perpendicular line falls on the A point), the point where the perpendicular falls satisfies the conditions for H. (I think all such points actually form a circle with AP’ as the diameter, where P’ is the parallel projection of P to the given plane, but I’m not 100% sure)
DUH! If this was math.stackexchange I’d choose this as answer
We percieve the 3 dimensions we exist in, through a 2d mapping, i.e. our retinas. So I think we are limited in how much of 3d we can really grasp at a time.
So Don’t we need more education about the 3D space in highschools really?
How often do you think most people need to know the advanced mathmatical properties of 3d space?
I mean, we live in it. It comes up in practice fairly often.
We use plenty of simple geometry everyday, sure, but you don’t need to be able to even understand what OP’s example says to engage with the world. Like you don’t need to provide a mathematical proof to put a shelf up properly.
Besides understanding what a projection is, I’m actually going to say that’s all pretty important stuff to know. A point, forming a line between points, how to describe a plane and what perpendicular means.
If you want to do graphics projections suddenly become very important, but sure, you can explain carpentry without it. Although if you want to draft the solution first the concept will be at least relevant.
Like you don’t need to provide a mathematical proof to put a shelf up properly.
Kind of a separate issue yet. Even with OP’s example, you can explain the solution in natural language pretty easily, but the obvious way to formally prove it would be with linear algebra.
How many people do you think are working in computer graphics? It’s specialised knowledge, exactly the kind of thing that should be taught at university to the people it’s relevent to.
you can explain the solution in natural language pretty easily
It’s not about how you phrase the solution, it’s about needing the solution at all.
Yeah, agreed, but like I said most of this is not advanced or specialised.
I think it is a shame that I’m a math student in university and needed to verify about such a thing. And if we’re talking about people doing physics it might be even worst if they suck like me at 3d geometry.
Math students in university need to verify basically everything, that’s a lot of what the career is about. I remember being humbled when asked to prove something as familiar to everybody as -1 * -1 = 1
hhhh abstract algebra and proof writing courses.
No for an orthogonal projection, because literally every point in the plane centered at H and normal to (AH) (so dihedrally perpendicular to the plane given in the problem) could potentially be P. In other words, it could project to H, or a point off of P perpendicularly to (AH)
You don’t really need math for that one, it’s just spacial reasoning, which you can’t really directly teach. I suppose just the concept of solid angle vs. dihedral angle vs. face angle would be good for everyone to know. To formally prove it, it seems like you’d need linear algebra, which they don’t usually teach in high school anyway.
Now, if you can use oblique projections as well, it’s pretty trivial to find one that’s “tilted” such that any point not already in the plane maps to a given H - the projection can proceed along any set of parallel lines through the space, and there’s always a line between any point X and H. Mathematically, you use the fact that X-H must be in the kernel space of the projection, and the standard formula for constructing a projection operator from a basis complementary to the kernel space and one in the plane it projects to.
I couldn’t make sense of the first paragraph, are you sure it is right ?
Pretty sure, yes. I’m probably just explaining badly.
There’s a full 360 degrees of rays perpendicular to (AH) starting at H. That would be true of line to a point in 3D. In 2D there would be exactly 2 possibilities (left and right), while in 4D they would correspond to an ordinary sphere, and hyperspheres in higher dimensions yet.
Together, they take up a plane. Only points on a certain (infinite) line going through this new plane and H will actually orthogonally map to H, and it’s the same one that’s normal to to original plane. Let’s call the line L.
If point P wasn’t in this plane, (PH) couldn’t be perpendicular to (AH). It is in the new plane, but we still don’t know for sure it’s on line L, so it’s not true that that implies it projects to H.
I tried again, I don’t find mistakes in your statements, I just don’t see how they make up for “instant in-mind proofs” for the problemI think I see it now, nevermind. Your got a very good visualization for 3D CanadPlus. It seems so intuitive that “the set of points that map to H with orthogonal projection is a straight line”, but do you happen to have a pocket proof for that ?Uhh, that the preimage of a point like H is a line? Off the top of my head, I’d use the fact it’s a shifted copy of the kernel. Well, assuming without loss of generality that we’re in a vector space and not just an affine space.
Using basic rules and notions from linear algebra and the theory of functions:
For a projection O in space V, your preimage L is defined as {l∈V | O(l) = H}. Using the linearity of O you can turn that into {l∈V | O(l-H) = 0}, which is equivalent to {y∈V | O(y) = 0} by setting l=y+H. Definitionally, an affine subspace is constructed from the members of a subspace added to a constant like that. The kernel, {y∈V | O(y) = 0}, is a subspace because any linear combination of vectors within it will, once you apply and distribute the operator using linearity again, turn into a sum of 0s, meaning the result must always be another member of the kernel.
All that’s left is to prove it’s a 1D affine subspace, AKA an infinite line. Every point w in the domain V is in some preimage, by the definition of a function, and so using the same math you can construct it as O(w)+k for some k in the kernel. O(r)=r for all r in the range by the definition of a projection, which you can use to both show it’s a subspace and can’t contain any basis of the kernel (expanding that out I’ll leave as an exercise). So, the dimension of the range and the kernel have to add to that of the whole domain. This actually holds for all other linear operators as well.
Our space is 3D and the provided plane is 2D. 3-2=1, QED.
Probably there’s a proof from the axioms of Euclidean geometry that doesn’t need linear algebra, but I was never good at that sort of thing. It’s also worth noting that any set defined purely by linear operators and affine linear subspaces will again be (describable as) affine linear. It’s like a closure property.
How first reading felt:
How the second reading felt at the beginning:
How it ended up:
What is{y∈V | O(y) = 0}? If the plane doesn’t pass through $0_V$ then how would that 0 be the image of some point ? Most likely you’re using something from linear algebra that I didn’t learn in my course (I didn’t learn projection I think, only examples when learning matrices).If the plane doesn’t pass through $0_V$ then how would that 0 be the image of some point ?
Answer, at risk of making it worse:
I was assuming this is a linear projection in a (non-affine) vector space, from the beginning. All linear operators have to to map the origin (which I’ve just called 0; the identity of vector addition) to itself, at least, because it’s the only vector that’s constant under scalar multiplication. Otherwise, O(0)*s=O(0*s) would somehow have a different value from O(0). That means it’s guaranteed to be in the (plane-shaped) range.
I can make this assumption, because geometry stays the same regardless of where you place the origin. We can simply choose a new one so this is a linear projection if we were working in an affine space.
Can I ask why you wanted a proof, exactly? It sounds like you’re just beginning you journey in higher maths, and perfect rigour might not actually be what you need to understand. I can try and give an intuitive explanation instead.
Does “all dimensions that aren’t in the range must be mapped to a point/nullified” help? That doesn’t prove anything, and it’s not even precise, but that’s how I’d routinely think about this. And then, yeah, 3-2=1.
(I didn’t learn projection I think, only examples when learning matrices).
Hmm. Where did the question in OP come from?
They’re abstractly defined by idempotence: Once applied, applying them again will result in no change.
There’s other ways of squishing everything to a smaller space. Composing your projection to a plane with an increase in scale to get a new operator gives one example - applied again, scale increases again, so it’s not a projection.
It sounds like you’re just beginning you journey in higher maths
I’m actually old and lurked in university stuff for a long time and dropped out of engineering in university and started with math all anew, yet at the same time I’m still a beginner.
Hmm. Where did the question in OP come from?
I don’t exactly remember How I started thinking about the “distance between plane and a point formula”, I think I stumbled upon it while organizing my old bookmarks. Tried to make a proof, and in the process that question came, and when I couldn’t solve it on the fly I though like “it’s so over for me”. Then ChatGPT also got it wrong and was like “It’s so over for mankind”. And I ended up making this post to share my despair. Actually many answers were eye opening.
Well see, here you have good proof that chatGPT isn’t actually “the best knowledge retrieving tool at the moment”. ChatGPT (and every other LLM) suuuucks at complicated math, because these text extruders don’t reason. Seriously, try out some more complicated math problems. I think you’ll find chatGPT gets most of them wrong, and in infuriating ways that make very little sense.
I don’t disagree that we need better math instruction for students. I’ve been saying this since I was a student. But using chatGPT being horrible at math as evidence of this is, well, ridiculous, frankly. ChatGPT’s performance isn’t based on how well your average high schooler understands something, and I don’t know why you’re trying to tie those two very different things together.
ChatGPT is trained based on forum discussions and pretty likely pirated books. If it found the idea in a previously established text it would have answered correctly. That’s why I DO think it is representative of what the average good student was taught (not how smart, or good at problem solving they be). What’s funny is that after reasoning it found the right answer, which is counter intuitive, since ChatGPT is supposed to be good at retrieving information, not at reasoning!
I’m trained on pirated books and I do alright.
Believing forum shitposts would definitely poison the well though.
when I say forums, that includes math.stackexchange, please don’t call it shitpost, people there are really something to say the least.
I didn’t say they were all shitposts. Just that it likely consumed shitposts.
